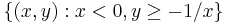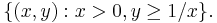Separating axis theorem
For objects lying in a plane (2-dimensional space), the separating axis theorem states that, given two convex shapes, a line onto which their projections are separate exists if and only if they do not intersect. A line for which the objects have disjoint projections is called a separating axis. An equivalent way of stating the theorem is to say that two convex shapes in the plane are not intersecting if and only if a line can be placed with one shape to one side of the line and the other shape to the other side. Such a separating line will be perpendicular to a separating axis.
For three-dimensional space, an axis can be found where the projection of two convex shapes can be separated if and only if they are not intersecting. In 3D, lines and planes are duals, and you can thus turn the separating axis theorem for 3D into the separating plane theorem. The general result in n dimensions is called the separating hyperplane theorem. This theory is due to Hermann Minkowski. The Hahn-Banach separation theorem generalizes the result to topological vector spaces.
A related result is the supporting hyperplane theorem.
Contents |
Uniqueness
Separating axes are not unique, as any line parallel to a separating axis is also a separating axis. Further, if the convex sets are compact, they will be separated by a positive distance on a separating axis, and thus any line whose slope is close enough to the separating axis will also be a separating axis.
Separating lines may be unique, if the sets are distance 0 apart (properly, if there are points in each that are arbitrarily close to points in the other) – for instance, if one set is the open left half-plane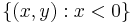 
and the other is the open right half-plane 
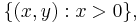then the y-axis 
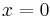is the only separating line. This can also hold for closed sets (if unbounded), if the sets are
However, for compact sets, separating lines are not unique: non-intersecting compact sets are a positive distance apart, by applying the extreme value theorem to the distance between points. Thus given a separating line between compact sets, a close enough parallel line will also be a separating line: visually, there is wiggle room.
Use in collision detection
The separating axis theorem says that if two convex objects are not penetrating, there exists an axis for which the projection of the objects will not overlap. This is an important definition because it suggests an algorithm for testing whether two convex solids intersect or not— in fact, it is heavily used in computational geometry, including computer games. It is also an important definition, because no matter what the dimensionality, the separating axis is always an axis — for example, in 3D, the space is separated by planes, but each plane is dual to a separating axis.
The separating axis theorem can be applied for fast collision detection between polygon meshes. Each face's normal or other feature directions is used as a separating axis, as well as the cross products. Note that this yields possible separating axes, not separating lines/planes.
If the cross products were not used, certain edge-on-edge non-colliding cases would be treated as colliding. For increased efficiency, parallel axes may be calculated as a single axis.
References
- Golshtein, E. G.; Tretyakov, N.V.; translated by Tretyakov, N.V. (1996). Modified Lagrangians and monotone maps in optimization. New York: Wiley. p. 6. ISBN 0471548219.
- Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nondifferentiable and two-level mathematical programming. Boston: Kluwer Academic Publishers. p. 19. ISBN 0792398211.